醋溜便当

题目背景

伊吹萃香是幻想乡的跟踪狂。

题目描述

萃香每天会派自己的分身巡视整个幻想乡。

幻想乡可以被视为一张 $n$ 个点 $m$ 条边的无向图，边有长度。萃香希望巡视到幻想乡的每个节点，于是她在每个节点 $i$ 都安排了一个分身，分身会沿着一条路径从 $i$ 出发再回到 $i$。可以多次经过同一条边，也可以多次经过同一个点（包括 $\bm i$）。

如果分身巡视的路径太短，会被居民怀疑有跟踪的风险；如果路径太长，又增大了每个分身的工作量。于是萃香希望回路的长度在 $[x,k\times x]$ 之间。$x,k$ 均为整数，且 $k>1$。

不过不是每个分身都能找到这样的回路。于是萃香会对于每个节点询问，是否存在一条从该节点出发的回路，长度在 $[x,k\times x]$ 之间。

输入格式

第一行有四个整数 $n,m,x,k$，含义如题面所示。

接下来 $m$ 行，每行有三个整数 $u,v,w$，描述一条连接 $u,v$ 的无向边，边权为 $w$。

输出格式

输出共一行 $n$ 个整数，之间用空格隔开。对于第 $i$ 个整数，若点 $i$ 可以找到一条长度在 $[x,kx]$ 之间的回路，则输出 $1$；否则输出 $0$。

样例 #1

样例输入 #1

7 5 3 2
1 2 4
1 3 0
2 3 0
1 6 5
4 5 6

样例输出 #1

1 1 1 0 0 0 0

提示

样例解释

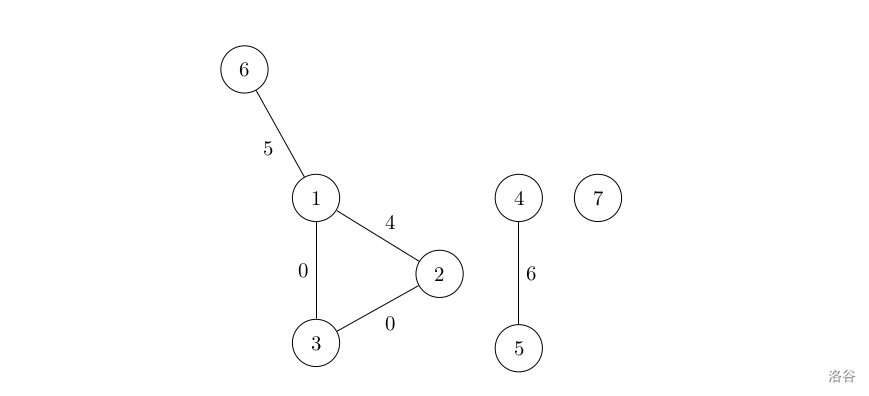
如图所示。对于前三个可以形成符合条件的回路的 $3$ 个点，可能的情况如下：

• $1:1\to 2\to 3\to 1$，长度为 $4$，在 $[3,6]$ 范围内；
• $2:2\to 3\to 1\to 2$，长度为 $4$，在 $[3,6]$ 范围内；
• $3:3\to 1\to 2\to 3$，长度为 $4$，在 $[3,6]$ 范围内；

对于剩下来的四个点：

• $4:$ 只能形成 $4\to 5\to 4,4\to 5\to 4\to 5\to 4,\cdots$，长度为 $12, 24, 36,\cdots$，无法形成 $[3,6]$ 内的回路；
• $5:$ 与 $4$ 的情况相同；
• $6:$ 与 $4$ 的情况相同；
• $7:$ 无法形成回路。

数据范围及约定

$$\def\arraystretch{1.5} \begin{array}{|c|c|c|}\hline \textbf{测试点} & \bm{n,m\le} & \textbf{特殊性质} \cr\hline 1\sim 6 & 20 & - \cr \hline 7\sim 10 & 10^3 & - \cr \hline 11\sim 12 & \text{无特殊限制} & \textbf{A} \cr \hline 13\sim 20 & \text{无特殊限制} & - \cr \hline \end{array} $$

特殊性质 $\textbf{A}$：保证边权均为正数。

对于全部数据，$1\le n,m\le 2\times 10^5$，$0\le w_i\le 10^9$，$1\le x\le 10^9$，$1<k\le 10^9$，并且有 $1\le x\times k\le 10^9$。