提桶跑路

题目背景

黑古山女是蜘蛛妖怪。因为是土蜘蛛，所以非常擅长土木工程。

题目描述

黑谷山女需要建造一张大网。

大网大体上可以分为一块矩形区域的网，以及用来加固的四根线。在不同的位置建造蛛网，建造出的强度各有不同。

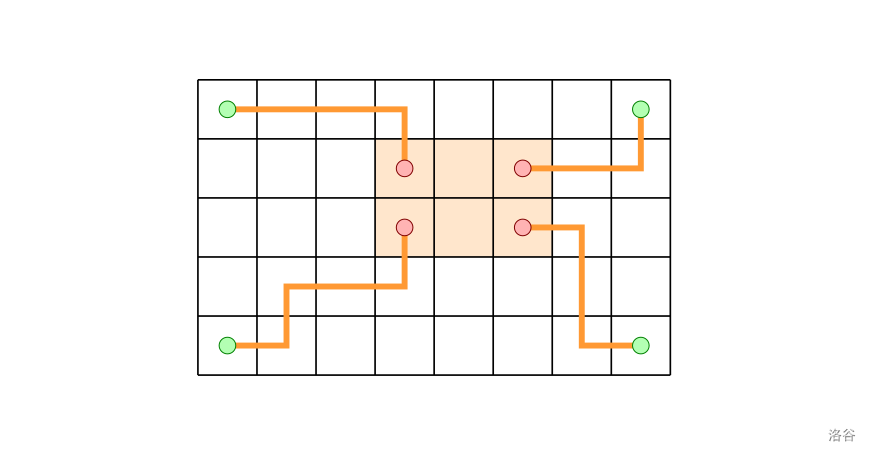
黑谷山女计算出了大小为 $n\times m$ 的权值矩阵 $a$。她会用如下方式构建方案：

• 选取 $a$ 的一个以 $(x_1,y_1)$ 为左上角，$(x_2,y_2)$ 为右下角的矩阵。子矩阵的长宽均不能小于 $\bm 2$。计算子矩阵内元素的和 $s_0$。
• 找一条从 $(x_1,y_1)$ 出发，终点为 $(1,1)$ 的路，每步只能向上走或者向左走。计算出路径内元素的和 $s_1$。元素和不包含 $(x_1,y_1)$ 位置。
• 找一条从 $(x_1,y_2)$ 出发，终点为 $(1,m)$ 的路，每步只能向上走或者向右走。计算出路径内元素的和 $s_2$。元素和不包含 $(x_1,y_2)$ 位置。
• 找一条从 $(x_2,y_1)$ 出发，终点为 $(n,1)$ 的路，每步只能向下走或者向左走。计算出路径内元素的和 $s_3$。元素和不包含 $(x_2,y_1)$ 位置。
• 找一条从 $(x_2,y_2)$ 出发，终点为 $(n,m)$ 的路，每步只能向下走或者向右走。计算出路径内元素的和 $s_4$。元素和不包含 $(x_2,y_2)$ 位置。

计算出该方案的总价值 $S=s_0+s_1+s_2+s_3+s_4$。

现在需要最大化 $S$ 的值。请输出最大的 $S$。

输入格式

第一行有两个整数 $n,m$，表示矩阵的大小。

接下来 $n$ 行，每行有 $m$ 个整数，描述矩阵内的元素。

输出格式

输出共一行一个整数，表示最大的 $S$ 的值。

样例 #1

样例输入 #1

4 4
1 -1 -1 1
1 1 1 1
1 1 1 1
1 -1 -1 1

样例输出 #1

12

样例 #2

样例输入 #2

9 6
-7 -10 -8 -1 -1 0
-2 0 -10 -2 -4 -2
-3 -2 1 2 8 0
4 -3 8 6 3 7
-6 9 -2 -1 10 0
-1 -2 -1 0 -2 8
-3 9 -2 5 5 4
-5 -3 -1 6 8 4
-5 0 0 0 -7 -3

样例输出 #2

65

提示

数据范围及约定

$$\def\arraystretch{1.5} \begin{array}{|c|c|c|}\hline \textbf{测试点} & \bm{n,m\le} & \bm{|a_{i,j}|\le } \cr\hline 1\sim 4 & 10 & 10 \cr\hline 5\sim 8 & 50 & 10^3 \cr\hline 9\sim 14 & 80 & \text{无特殊限制} \cr\hline 15\sim 16 & \text{无特殊限制} & 10^3 \cr\hline 17\sim 20 & \text{无特殊限制} & \text{无特殊限制} \cr\hline \end{array}$$

对于全部数据，$2\le n,m\le 400$，$0\le |a_{i,j}|\le 10^9$。