#418. 爷是阿吽
爷是阿吽
爷是阿吽
题目背景
高丽野阿吽是具有两种动物特性的在博丽神社看门的神兽。由于设定上是对应一对神兽,因此呈现出了两种不同的特质。
因为天天看门很无聊,于是阿吽找来了一堆棋子。棋子之间互相联系,形成了一棵树(×1 不用在意为什么会变成一棵树)。
棋子有正反两面。正面写有数字,背面没有东西。阿吽会按照一定规则对棋子进行翻转,而你需要计算出所有写有能被看见的数字的最大值。
题目描述
给定一棵有 个节点的有根树,树的根为 。树上每个节点有点权 。此外,每个节点还会有状态 。
现在有 次操作。每次操作会选择节点 ,接着:
- 若 的状态为 ,则将 的状态置为 ;
- 将 的状态为 ,则将 的状态置为 ,同时将所有 节点的儿子节点的状态置为 。
在所有操作之前,以及每次操作之后,输出「所有状态为 的节点,权值的最大值」。特别地,若此时没有状态为 的节点,请输出 。
输入格式
第一行有两个整数 ,分别表示这棵树的节点个数以及操作个数。
接下来 行,每行两个整数 ,表示树的一条边。
接下来一行有 个整数,第 个整数给出 的值。
接下来一行有 个整数,第 个整数给出 的初始值。
接下来 行,每行有一个整数 ,描述这次操作的节点。
输出格式
输出共 行,表示每次询问的结果。
样例 #1
样例输入 #1
11 5
1 2
1 8
1 9
2 3
2 4
9 10
9 11
4 5
4 6
4 7
7 4 5 2 3 3 6 5 3 4 1
1 0 0 0 0 1 0 0 1 0 1
1
8
2
4
1
样例输出 #1
7
5
4
5
6
7
提示
样例解释
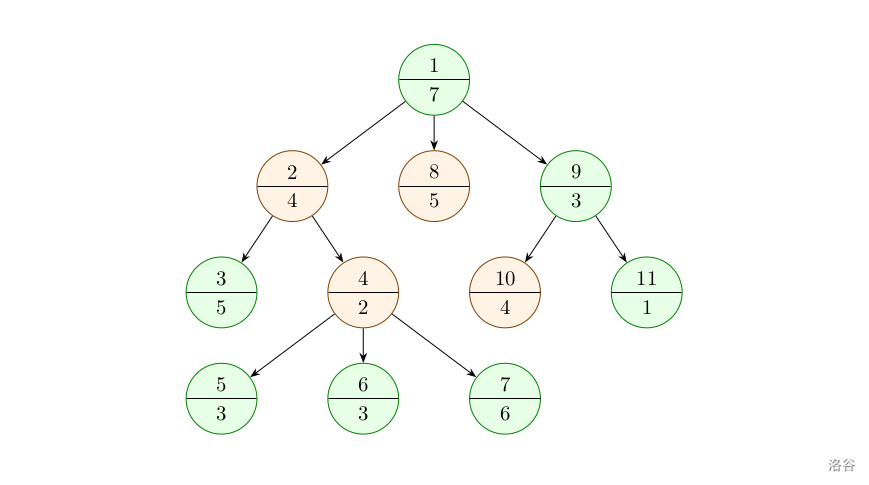
初始情况如下图所示。绿色节点表示状态为 ,橙色节点表示状态为 。节点上半部分是节点序号,下半部分是节点权值。
此时最大值为 。
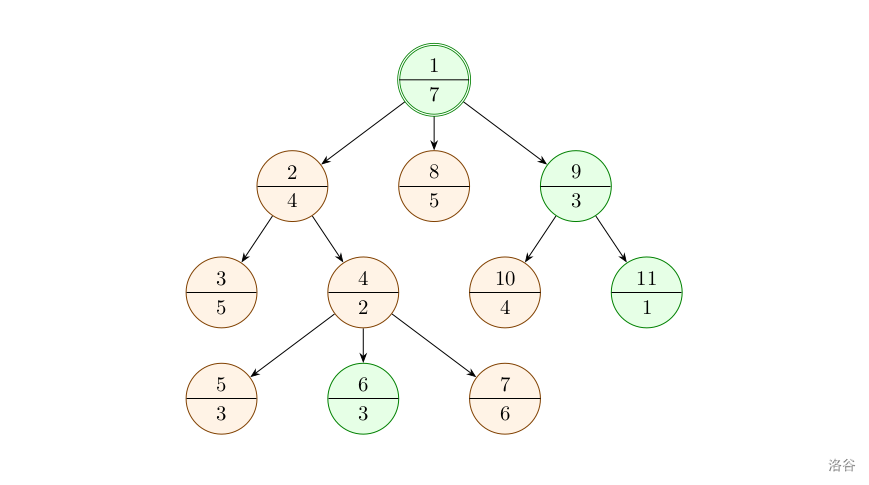
对节点 进行操作后, 的状态变为 , 的状态变为 。 的状态没有发生改变,仍为 。
此时最大值为 。
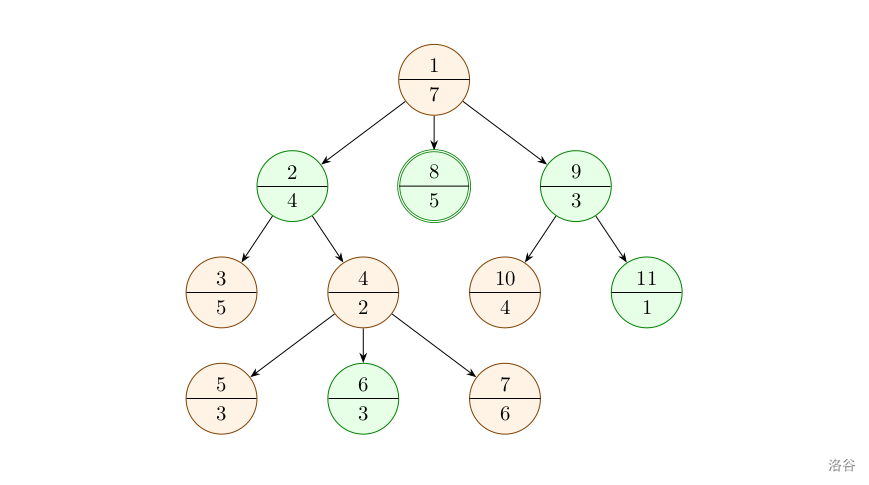
对节点 进行操作后, 的状态变为 。
此时最大值为 。

对节点 进行操作后, 的状态变为 , 的状态变为 。
此时最大值为 。
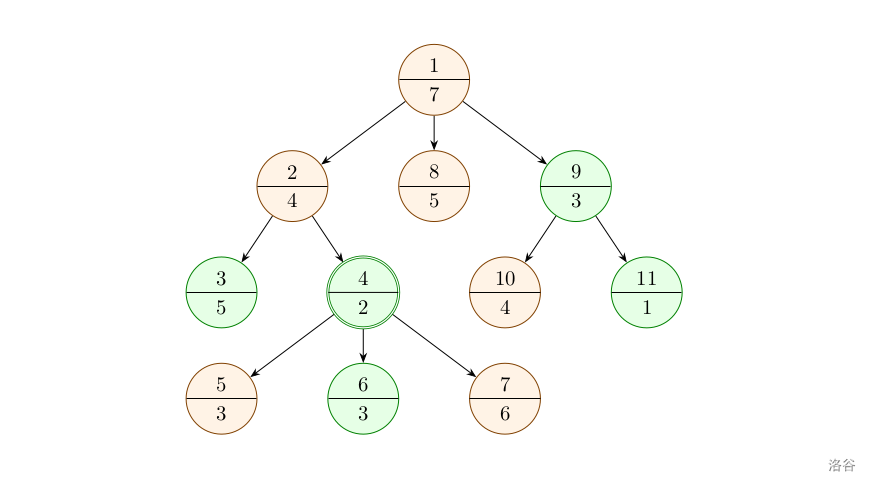
对节点 进行操作后, 的状态变为 , 的状态变为 。
此时最大值为 。
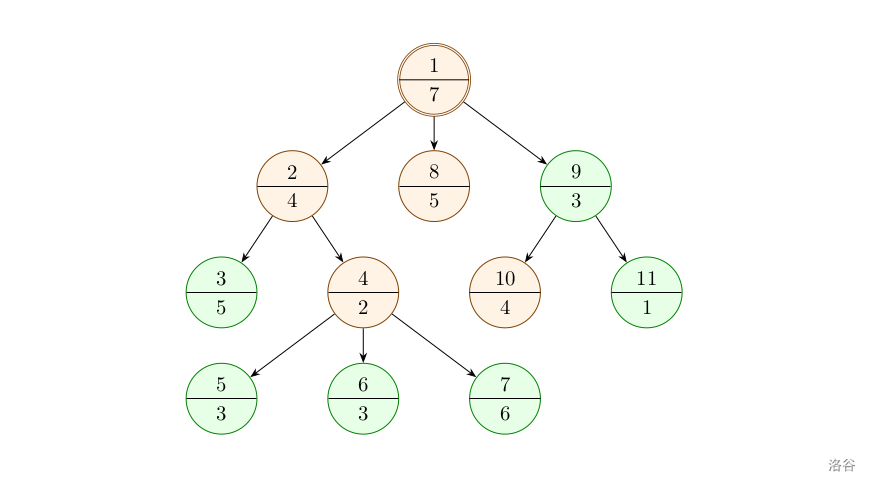
对节点 进行操作后, 的状态变为 。
此时最大值为 。
数据范围及约定
$$\def\arraystretch{1.5} \begin{array}{|c|c|c|c|}\hline \textbf{测试点} & \bm{n\le } & \bm{m\le } & \textbf{特殊性质} \cr\hline 1 & 1 & 0 & - \cr\hline 2\sim 3& 100 & 100 & - \cr\hline 4\sim 6 & 5\times 10^3 & 5\times 10^3 & -\cr\hline 7 & \text{无特殊限制} & \text{无特殊限制} & \textbf{A} \cr\hline 8 & \text{无特殊限制} & \text{无特殊限制} & \textbf{B} \cr\hline 9\sim 10 & \text{无特殊限制} & \text{无特殊限制} & - \cr\hline \end{array}$$特殊性质 :原图是一条链,并且 号节点是链的一个端点。 特殊性质 :原图是菊花图,并且 号节点是菊花图的中心。
对于全部数据,,。
:新增加 组 数据。 数据的约束条件如下:
$$\def\arraystretch{1.5} \begin{array}{|c|c|c|c|}\hline \textbf{Hack} & \bm{n\le } & \bm{m\le } & \textbf{特殊性质} \cr\hline 1 & 5\times 10^3 & 5\times 10^3 & \textbf{A} \cr\hline 2& 5\times 10^3 & 5\times 10^3 & \textbf{B} \cr\hline 3 & 5\times 10^3 & 5\times 10^3 & -\cr\hline 4 & \text{无特殊限制} & \text{无特殊限制} & \textbf{A} \cr\hline 5 & \text{无特殊限制} & \text{无特殊限制} & \textbf{B} \cr\hline 6 & \text{无特殊限制} & \text{无特殊限制} & - \cr\hline \end{array}$$
