思路

抽象一下题意 我们发现问题是：
把n拆分为两个正整数之积 
使这两个正整数之和减2最小

$于是我们有了最初想法 O（n^2）$

//暴力枚举
for (i = 1 ~ n)
      for (j = 1 ~ n)
           if (i * j == n)
              //操作

我们可以发现
只要找到n的第一个因数
那么第二个也随之确定
并且 我们发现
那个比较小的因数 一定<=sqrt(n)
(对于正整数n 大于sqrt_n的因数只有一个)
我们只需要枚举这个就可以

稳定$O(\sqrt{n})$

结论：最接近$O(\sqrt{n})$的两个因数之和最小

(接下来是数学证明 可以不看) $设n = ab(a != b), n = c^2，$(a + b)^2 - (2c)^2$$= a^2 + 2ab + b^2 - 4c^2$$= a^2 - 2ab + b^2$$= (a - b)^2 >= 0$所以$(a + b)^ 2 >= (2c)^2$$即 a + b >= 2c$这样$我们就证明了2个\sqrt{n}之和最小$因为$(a - b)^2 >= 0$所以$随着a与b差的增大 (a - b)^2单调递增（无论a, b怎么取）$即$a + b 越来越大 （c不变）$**证毕**$大概描述一下 当n确定时 横坐标为a, 纵坐标为a + b$$样子大概是y = (x - \sqrt{n})^2 + 2\sqrt{n}那样$ 但是要强调 并不是平方级增长 我只是描述这个趋势

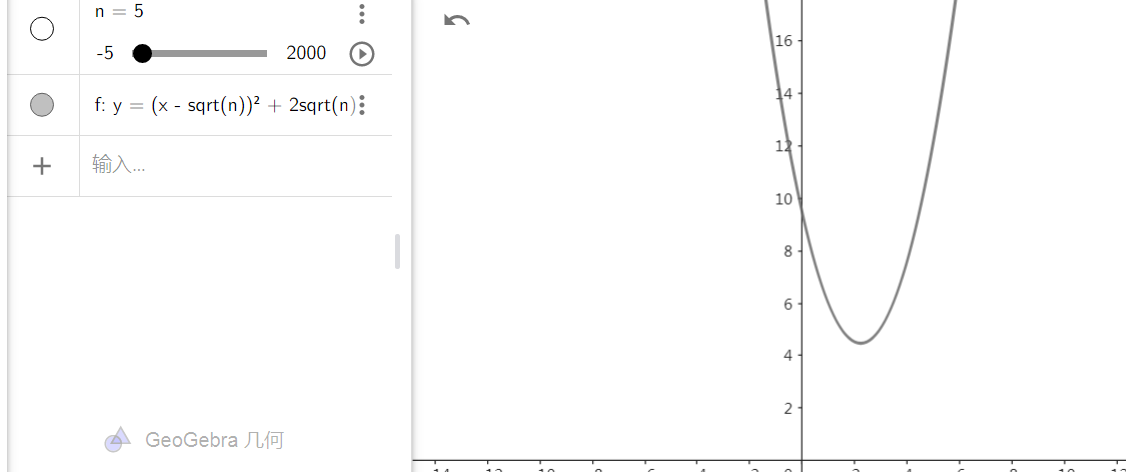最坏$O(\sqrt{n})$

AC代码

#include <iostream>
#include <cstring>
#include <cmath>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long LL;

LL n, ans;

int main()
{
    scanf("%lld", &n);

    LL sqrt_n = sqrt(n);
    for (LL i = sqrt_n; i; -- i)
    {
        LL j = n / i;
        if (i * j == n)
        {
            ans = i + j - 2;
            break; 
        }
    }

    printf("%lld\n", ans);

    return 0;
}